Probabilistic Graphical Models(9)

17~23为Octave语言教学。Octave是GNU开源项目，语法类似于MATLAB，更轻量级，同时具有CLI和GUI两种形式，适合于科学计算与早期算法实现。

024_Overview of Structured CPDs

本节介绍了CPD（条件概率分布）的几种结构化表示形式和特定背景独立性（Context-Specific Independence）的概念。

条件概率表最典型的表示方式是表格表示（Tabular Representations），如图1所示。一般而言，若有k个父变量（且为二值变量），子变量的CPD表格中就需要有2的k次方个表项。

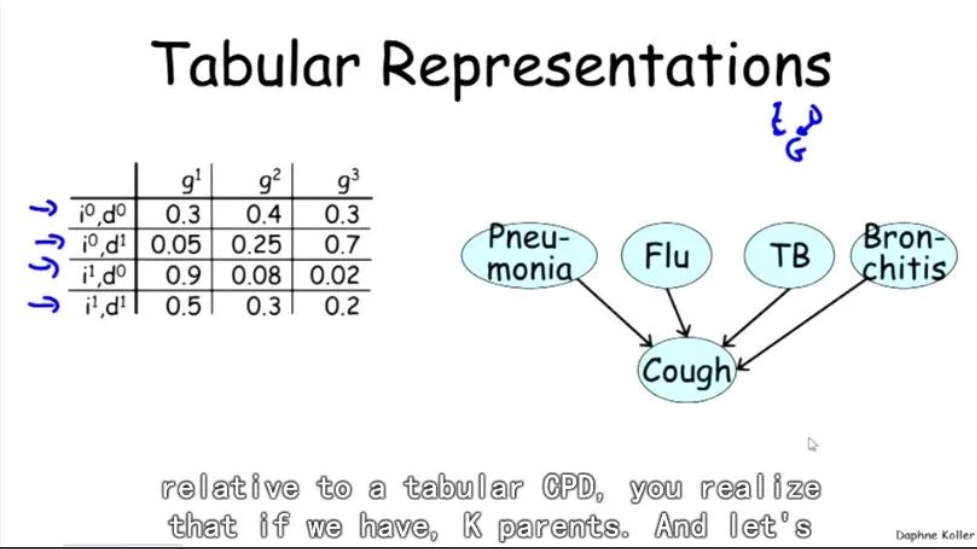
图1 表格式表示

从CPD的定义出发，只要满足：一个函数可以描述变量x在每种y1~yk的组合上的概率；且总概率和归一，就是CPD。因而可以拓宽CPD的形式。图2给出了一些常见的CPD形式，包括确定性函数CPD和之后将要讲解的树形结构CPD，最后一种线性高斯用于连续性情况。

图2 其他CPD

Context-Specific Independence：基于特定背景的一种条件独立，在图3给出的形式化定于中可以看出：在变量Z和变量C取特定值c的条件下，X与Y相互独立。此独立还可以衍生出图3下方的三个推论。

图3 Context-Specific Independence

为了加深理解，课程中给出一道简单例题（图4）。第二项和第三项满足Context-Specific Independence，因为在给定的条件下，我们无法由其中一个变量的状态得到更多关于另一变量状态的信息（相互独立）。

图4 小例题

025_Tree Structured CPDs

本节详细介绍了树形结构的CPD，树形结构CPD通过变量间的相互依赖压缩了存储的数据量。此外，还介绍了Multiplexer CPD（多路选择CPD）和其应用。

图5给出了树形CPD的示例，Apply、SAT和Letter共同决定是否可以得到工作，结果元组的第一项是被拒绝的概率，第二项是被接受的概率。需要注意的是：该树形CPD在绘制时考虑了变量之间的依赖关系，所以最后的结果项从8项压缩到了4项。

图5 树形结构CPD

观察树形结构的CPD，我们可以更方便地看出变量之间的依赖关系。同上一节一样，课程中给出一道判断独立性的小例题（图6），结果比上一题更显然。

图6 小例题2

Multiplexer CPD：多路选择CPD。此处以图7的树形CPD为引入，变量Choice的值决定了变量L1和L2的取值（选择L1还是L2）。类比数字电路中的多路选择器。

图7 树形结构CPD示例2

图8给出了这类多路选择CPD的内部示意图，变量A决定了变量y选择Z的哪一个副本作为自己的值。

图8 多路选择CPD

类似的理念在其他许多场景下也有应用，如微软的Troubleshooters就有这样的选择结构。总结来说，使用特定背景下的依赖关系，可以压缩CPD的表示；相关性在硬件配置、医疗环境等诸多场合下被应用。

图9 总结